When visualizing geospatial data in densely built-up areas, the display of large quantities of data points on a map can be obscured due to the close proximity of each data point. For example, transactional data on the sale of different apartment units in the same building can result in the gross overlap of data points when visualized spatially. This is because (at least for the case of Singapore) the apartment units share the same postal codes, and thus, will be geocoded to the same geographical coordinates.

One possible solution to this is to spread out the overlapping data points in a random, normally distributed manner around the original coordinates. Doing so will better help visualize the "concentration" of an event occurring around the given point, rather than simply displaying a single point. The variance will have to be chosen carefully so as to prevent excessive dispersal of data points, to the extent that it renders the visualization completely inaccurate.

For each (overlapped) coordinate, the coordinate will be shifted a random distance Y meters along latitudes (North-South direction) and a random distance X meters along longitudes (East-West direction). The coordinates of the shifted position are then calculated using the Haversine formula.

skip to visualization

The Haversine Formula

Where d is distance between the two points (x_1, y_1), (x_2, y_2) in meters. R represents the radius of the Earth in meters. x_1, x_2, y_1, y_2 are expressed in radians.

\sin^2 (\frac{d}{2R}) = \sin ^2(\frac{y_2-y_1}{2}) + \cos(y_1)\cos(y_2)\sin^2 (\frac{x_2-x_1}{2})

d=2R\sin ^{-1}\Bigg(\sqrt{\sin ^2(\frac{y_2-y_1}{2}) + \cos(y_1)\cos(y_2)\sin^2 (\frac{x_2-x_1}{2}})\Bigg)

The following code calculates the distance between two points given their coordinates in degree decimals. This general haversine formula function will be useful later.

import math
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure

def haversine(lat1, lon1, lat2, lon2):
    '''
    Haversine formula to calculate great circle distances between two points
    latitude and longitude in degree decimals.
    Radius of Earth used is equatorial radius of 6378.1370km
    Returns distance between the two coordinates (lat1, lon1), (lat2, lon2) in meters
    '''
    R = 6378137
    lat1 = math.radians(lat1)
    lat2 = math.radians(lat2)
    lon1 = math.radians(lon1)
    lon2 = math.radians(lon2)
    
    distance= 2*R*math.asin(math.sqrt(math.sin((lat1 - lat2)/2)**2 + math.cos(lat1) * math.cos(lat2) * math.sin((lon2-lon1)/2)**2))
        
    return distance
    

# Example: Distance between Singapore Zoo and Marina Bay Sands

lat1, lon1 = (1.4033998,103.7891814) #Singapore Zoo
lat2, lon2 = (1.2833808,103.8585323) #Marina Bay Sands

print("{} meters.".format(haversine(lat1, lon1, lat2, lon2)))

  15429.484755676576 meters.

The Haversine Formula is more generally used to calculate great circle distance between two points on a sphere (i.e., the Earth). However, our goal now is to derive the coordinates of a new point, given that we have the starting coordinates and the distance shifted laterally ( Y ) and longitudinally ( X ). This still can be achieved using the same formula, with a little bit of manipulation.

Re-arranging the Haversine Formula

First, we will obtain the coordinates of an intermediary point after shifting the original point laterally (North-South direction) with distance Y. Since d=Y is known, the original coordinates (x_1,y_1) are known, and the longitude of the intermediary point remains unchanged, (x_1=x_2). The only unknown variable left is y_2. Re-arrange the Haversine Formula below and solve for y_2.

From \ (1)

\sin^2(\frac{Y}{2R}) = \sin ^2(\frac{y_2-y_1}{2}) + \cos(y_1)\cos(y_2)\sin^2 (0) \\

2sin^{-1}\Big(\sqrt{\sin^2(\frac{Y}{2R})}\Big) = y_2 - y_1 \\

y_2 = y_1 + 2sin^{-1}\Big(\sqrt{\sin^2(\frac{Y}{2R})}\Big) \\

The following code block for get_new_lat() calculates this.

def get_new_lat(distance, lat1):
    
    '''
    Given "vertical" distance in meters (traverse latitude), while holding longitude constant,
    and latitude in degrees decimal
    return new latitude in degrees
    
    Negative distance -> Move South
    Positive distance -> Move North
    '''
    sign = -1 if distance < 0  else 1
    R = 6378137
    A = math.sin(distance/(2*R))**2
    lat2 = math.radians(lat1) + 2*math.asin(sign*math.sqrt(A))
    lat2 = math.degrees(lat2)
    
    return lat2
    

Likewise, repeat the same and shift the new intermediary point longitdudinally.

From \ (1)

\sin^2(\frac{X}{2R}) = 0 + \cos(y_1)\cos(y_2)\sin^2 (\frac{x_2-x_1}{2}) \\

\frac{\sin^2(\frac{X}{2R})}{\cos^2(y_1)} = \sin^2 (\frac{x_2-x_1}{2}) \\

\sin^{-1}\Big(\sqrt{\frac{\sin^2(\frac{X}{2R})}{\cos^2(y_1)}}\Big) = \frac{x_2-x_1}{2} \\

x_2 = 2 \sin^{-1}\Big(\sqrt{\frac{\sin^2(\frac{X}{2R})}{\cos^2(y_1)}}\Big) + x_1

The following code block for get_new_lon() calculates this.

def get_new_lon(distance, lat1, lon1):
    
    '''
    Given "horizontal" distance in meters (traverse longitude), while holding latitude constant,
    and longitude in degrees decimal,
    return new longitude in degrees
    
    Negative distance -> Move West
    Positive distance -> Move East
    
    '''

    sign = -1 if distance < 0  else 1
    R = 6378137
    A = math.sin(distance/(2*R))**2
    lat1 = math.radians(lat1)
    lon1 = math.radians(lon1)
    lon2 = 2*math.asin(sign*math.sqrt(A/(math.cos(lat1)**2))) + lon1
    lon2 = math.degrees(lon2)

    return lon2
    

Bringing both get_new_lon() and get_new_lat() functions together, we get move_to_new_coordinate() that calculates the coordinates of a new point given the distance travelled longitudindally and laterally.

def move_to_new_coordinate(lat1, lon1, lat_dist, lon_dist):
    '''
    Given distance to travel across longitudes in meters (lon_dist -> Along X-axis),
    Given distance to travel across latitudes in meters (lat_dist -> Along Y-axis),
    Return new coordinates in decimal degrees
    lat_dist, lon_dist negative values are valid.
    '''
    R = 6378137
    lat_sign = -1 if lat_dist < 0  else 1
    lon_sign = -1 if lon_dist < 0 else 1
    
    lat1 = math.radians(lat1)
    lon1 = math.radians(lon1)
    
    # Move laterally
    A = math.sin(lat_dist/(2*R))**2
    lat2 = lat1 + 2*math.asin(lat_sign*math.sqrt(A))
    lat2 = math.degrees(lat2)
    
    # Move longitudinally
    B = math.sin(lon_dist/(2*R))**2
    lon2 = 2*math.asin(lon_sign*math.sqrt(B/(math.cos(lat1)**2))) + lon1
    lon2 = math.degrees(lon2)
    
    return (lat2, lon2)

Generating random distances from point of origin

The next step we need generate random distances X and Y around the point of origin. Both X and Y will be distributed normally with 0 means and 0 covariances (independence).

\mathbf{X, Y} \sim \mathcal{N}(\mathbf{0}, \mathbf{\Sigma}) , \mathbf{\Sigma} = \begin{bmatrix} \sigma^2_x & 0 \\ 0 & \sigma^2_y \\ \end{bmatrix}

To ensure that the distances generated will not end up unreasonably far from the original point, we'll need to select an appropriate variance. What is an appropriate variance? It is one that ensures that your generated points fall within a comfortable distance from the original point.

For example, we would want to find out the probability of the new points landing within 500 meters of the original point. For short distances, the Pythagoras theorem works well enough (see spherical law of cosines).

P(X^2 + Y^2 \leq 500^2) = P\Big(\Big(\frac{X-0}{\sigma}\Big)^2 +\Big(\frac{Y-0}{\sigma}\Big)^2 \leq \frac{500^2}{\sigma^2}) = P\Big(Z^2_1 + Z^2_2 \leq \frac{500^2}{\sigma^2} \Big)

Z_1, Z_2 \sim i.i.d. \mathcal{N}(0,1) \quad \quad z = \frac{500^2}{\sigma^2}

P\Big(Z^2_1 + Z^2_2 \leq z \Big) = \iint_{Z^2_1 + Z^2_2 \leq z} \frac{1}{\sqrt{2\pi}}e^{\frac{-z_{1}^{2}}{2}} . \frac{1}{\sqrt{2\pi}}e^{\frac{-z_{2}^{2}}{2}} dxdy

= \frac{1}{2\pi}\iint_{Z^2_1 + Z^2_2 \leq z} e^{-(z^2_1 + z^2_2)/2} dxdy

Using polar coordinates,

= \frac{1}{2\pi}\int_{0}^{2\pi}\int_{0}^{\sqrt{z}} re^{-r^2/2} drd\theta

= \int_{0}^{\sqrt{z}} re^{-r^2/2} dr

Let u = r^2 ,

P\Big(Z^2_1 + Z^2_2 \leq z \Big) = \frac{1}{2}\int_0^z e^{-\frac{u}{2}} du

= 1 - e^{-\frac{z}{2}}

Choosing \sigma^2=50000 , z = \frac{500^2}{50000} = 5 . To know what is the probability of a new point landing within 500 meters of the orignal point, we calculate 1 - e^{\frac{5}{2}} = 0.917915

So the probability of a point landing within 500 meters of the original point is approximately 91.8% given \sigma^2=50000.

Let's verify this empirically.

# Example using variance of 50000, generate 10000 points

np.random.seed(123)
variance = 50000
figure(figsize=(4, 4), dpi=120, facecolor='w', edgecolor='k')

XY_distances = np.random.multivariate_normal(
    mean=[0, 0], 
    cov=[[variance,0],[0,variance ]], 
    size=10000
)

X = XY_distances[:,0]
Y = XY_distances[:,1]

graph = plt.scatter(X, Y, s=1)

plt.ylim(-1000, 1000)
plt.xlim(-1000, 1000)
plt.scatter(0, 0, s=30, c='r')

plt.show()

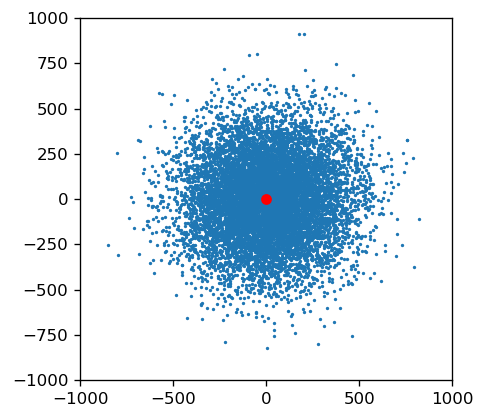
euclidean_distances = [ math.sqrt(x**2 + y**2) for x,y in XY_distances ]
n_within_500m = sum([ 1 if x<500 else 0 for x in euclidean_distances ])
prob_within_500m = n_within_500m / len(euclidean_distances)

print("% points falling within 500 meters: {}".format(prob_within_500m))

  % points falling within 500 meters: 0.9183

This is reasonably close and we can conclude that that the estimation is accurate. To generalize, if you want to find the variance \sigma^2_k that ensures p % of generated points falling within k meters from the original point, you calculate:

p = 1 - e^{-\frac{k^2}{2\sigma^2_k}}

\sigma^2_k = \frac{-k^2}{2ln(1-p)}

def get_dist_var(distance, p):
    '''
    Function to calculate variance that will ensure random point generated 
    will end up k meters away from origin point with probability p
    0 < p < 1
    '''
    return (-distance**2) / (2*math.log(1-p))

get_dist_var(500, 0.95) # variance where 99% of all points fall within 500m

  41726.02508691677

Putting it all together

Finally, we will put all the parts together in the function gen_disperse_points which will create an n x 2 array of new coordinates that are dispersed in a normally distributed manner around a given coordinate (lat1, lon2) and a given variance that controls the spread of the points.

def gen_disperse_points(lat1, lon1, n, var):
    
    '''
    Given coords of a point (lat1, lon1),
    generate n new coordinates that are randomly dispersed around (lat1, lon1)
    new coordinates are generated using a bivariate normal distribution of variance var
    Returns n x 2 array of new coordinates
    '''

    XY_distances = np.random.multivariate_normal(
        mean=[0, 0], 
        cov=[[var,0],[0,var ]], 
        size=n
    )

    new_coords = [ move_to_new_coordinate(lat1,lon1, dist[0], dist[1]) for dist in XY_distances ]
    
    return np.array(new_coords)

Case Study: Visualizing Private Housing Transactions in Singapore

To demonstrate a useful case for the dispersal of overlapping geospatial data points, we'll visualize all private residential transactions in Singapore for 2018. The dataset contains 23,390 transactions on a total of 5,933 unique postal codes which were geocoded to coordinates. Without any dispersion, only 5,933 points will be visible on the map as the remaining 17,457 data points will be obscured due to extensive overlapping.

The two visualizations show large differences. This is not surprising considering that three quarters of the data were hidden in the first visualization. The second visualization with dispersion is arguably a more useful representation of housing transactions on a map as it contains more information:

• The frequency/concentration of the event is accurately represented geographically. For example, areas where there are seemingly little transactions in the first visualization are revealed in the second one to have high density of transactions (see North-East region).


• Differences in transaction volumes can be compared across time using the same visualization with dispersion. Less dots on the map mean less transactions. This can be said for the second visualization (with dispersion) but not the first one.

The price of a more accurate visualization is a tradeoff in precision. The data points along the East Coast that end up in the sea are a case in point. Nevertheless, this is a small price to pay for a more visually informative map. In any case, the variance can be further fine-tuned to control the spread of the data points so as to suit the preference of the mapmaker.